Método de Puls
Quando se analisa o problema do abatimento de hidrogramas em reservatórios, depara-se com um problema de escoamento não permanente. O escoamento é caracterizado por uma grande profundidade e, consequentemente, baixa velocidade, de modo que os termos dinâmicos da equação dinâmica do escoamento são desprezíveis (TUCCI, 2007).
A forma amplamente difundida na bibliografia deve-se ao trabalho de Puls (1928) e Puls (1947), divulgado posteriormente de forma mais ampla como método de Puls modificado (BUTLER, 1957).
A água que entra no reservatório ao longo do tempo se refere a vazão afluente e fica temporariamente armazenada para sair pela tubulação, para então ser chamada de vazão efluente. Esta deve ser menor que aquela como decorrência do armazenamento. Essa redução de vazão é chamada de atenuação ou laminação. E o procedimento para calcular seu valor é chamado de propagação.
O Modelo de Puls caracteriza-se por supor que existe uma relação entre o volume armazenado e a vazão efluente, sendo esta, portanto, independente da vazão afluente. Isso equivale a assumir que a superfície do reservatório se mantenha plana e horizontal, o que é em muitos casos apenas uma aproximação dada a existência do remanso.
Para determinar a propagação dos cursos d’água em reservatórios, ou seja, bacias de detenção, o Método de Puls é amplamente utilizado. Ele consiste na equação da continuidade, que é um balanco da água que entra e da aguá que sai. Ele consiste na discretização do tempo, ou seja, passa-se de uma equação infinita (derivada) para finita (intervalo de tempo \(\Delta\)t), podendo ocorrer erros nos resultados devido a esse fato. Quanto maior a discretização de tempo maior as chances de ocorrer um erro. Nos exemplos utilizados é necessário que a vazão de pico seja um ponto na tabela de propagação, para isso temos que discretizar o tempo de uma forma coerente.
\begin{equation} \label{eq:eqcContinuidade1}\tag{1} I - O = \frac{\Delta S}{\Delta t} \end{equation}
Onde:
I: vazão média afluente ao reservatório durante o tempo \(\Delta\)t (\(m^3\)/s);
O: vazão média efluente do reservatório durante o tempo \(\Delta\)t (\(m^3\)/s);
\(\Delta\)S: variação no volume do reservatório durante o tempo \(\Delta\)t (\(m^3\));
\(\Delta\)t: período incremental (s).
Para resolver a equação \ref{eq:eqcContinuidade1}, primeiro reescreva para uma forma mais prática:
\begin{equation} \label{eq:eqcContinuidade2}\tag{2} \frac{I_{1}+I_{2}}{2}+\frac{O_{1}+O_{2}}{2}=\frac{S_{2}+S_{1}}{\Delta t} \end{equation}
Os subscritos 1 e 2 denotam o início e o fim, respectivamente, do período \(\Delta\)t escolhido. Os termos na equação \ref{eq:eqcContinuidade2} podem agora ser reorganizados como:
\begin{equation} \label{eq:eqcContinuidade3}\tag{3} \left (I_{1} + I_{2} \right ) + \left [\frac{2S_{1}}{\Delta t} - O_{1} \right ] = \frac{2S_{2}}{\Delta t} + O_{2} \end{equation}
Na equação \ref{eq:eqcContinuidade3}, todos os termos a esquerda são conhecidos de cálculos anteriores de propagação, enquanto os termos a direita são desconhecidos e devem ser determinados pela propagação em reservatório. Supõe-se, que:
- A superfície da água nesse método é horizontal;
- A vazão efluente é uma função única do volume de armazenamento;
- A vazão efluente varia linearmente com o tempo, durante cada período \(\Delta\)t.
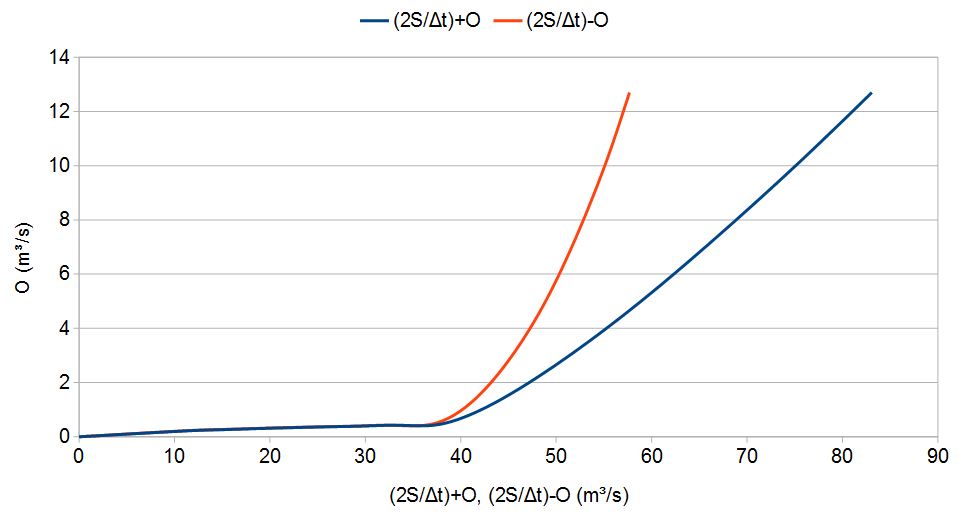
Com base na duração do ramo ascendente do hidrograma de entrada, um período \(\Delta\)t será escolhido. Então, é feito uma combinação dos termos conhecidos para criar duas relações: gráficos de O versus 2S/\(\Delta\)t + O e versus de 2S/\(\Delta\)t – O (figura 1) para achar a vazão de saída.
Figura 1: Gráfico de O versus 2S/∆t+ O e de O versus 2S/∆t– O
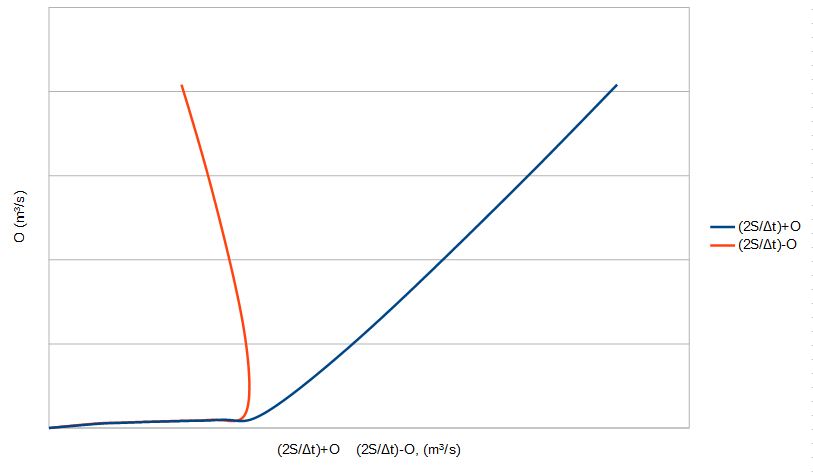
No projeto de uma bacia de detenção, a equação \ref{eq:eqcContinuidade3} é usada no calculo do hidrograma de saída quando se conhece o hidrograma de entrada. Esse cálculo constitui uma propagação. Se a bacia de detenção não produzir os resultados pretendidos, os parâmetros devem ser revisados, procedendo-se então a uma outra propagação. Assim, o processo é de tentativa e erro até calibrar os melhores parâmetros.
Aplicação do Modelo
Para aplicação do modelo foi dimensionado um reservatório para suportar o dobro da sua capacidade de volume que é aproximadamente 6.000 \(m^3\), área total construída de 5.157,12 \(m^2\), altura da arquibancada de 2,70m, com degraus de 80x45cm, cota da soleira do vertedouro de 1,50m, largura da soleira de 5m, para 4 orifícios de 30cm de diâmetro (figura 2 e 3).
Figura 2: Planta baixa do reservatório de 6.000 m³.
Figura 3: Vista do reservatório de 6.000 m³.
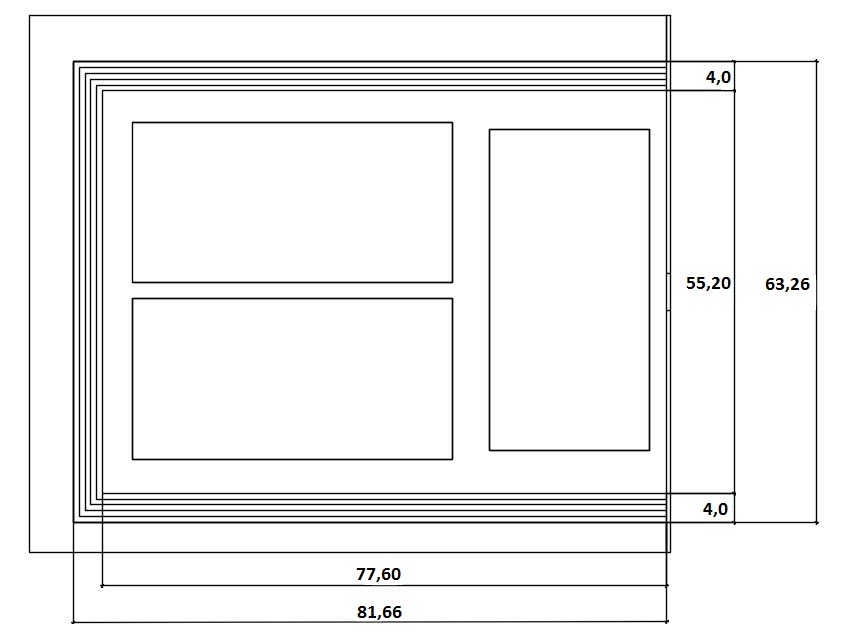
O diâmetro do orifício é algo que deve ser levado em consideração. É necessária a colocação de grelha para cobrir o tubo, como vivemos numa sociedade em que o vandalismo predomina, tubos com diâmetros muito grande podem representar perigo para os transeuntes, pois se arrancadas as grelhas, ficam buracos enormes nos quais uma criança pode cair durante uma chuva com uma lâmina d’água.
Segundo Gribbin (2009), o coeficiente de descarga, \(C_{d}\), é uma constante de proporcionalidade adimensional, responsável pela redução do fluxo em razão da perda de carga na entrada. O valor experimental de \(C_{d}\) para orifícios de borda reta varia de acordo com o tamanho, a forma e a quantidade de carga. No entanto, para a maioria das aplicações, resultados confiáveis podem ser obtidos com o uso de \(C_{d}\) = 0,62.
Com os dados de dimensionamento do reservatório, foi gerado a tabela 1 e gráficos (Anexo A) que relaciona a cota, área e volume.
| cota (m) | área (m²) | volume (m³) |
|---|---|---|
| 0 | 4283,52 | 0 |
| 0,45 | 4283,52 | 1927,58 |
| 0,6 | 4453,12 | 2582,83 |
| 0,75 | 4453,12 | 3250,8 |
| 0,9 | 4453,12 | 3918,77 |
| 1,05 | 4625,28 | 4599,65 |
| 1,2 | 4625,28 | 5293,44 |
| 1,35 | 4625,28 | 5987,23 |
| 1,5 | 4800 | 6694,13 |
| 1,65 | 4800 | 7414,13 |
| 1,8 | 4800 | 8134,13 |
| 1,95 | 4977,28 | 8867,42 |
| 2,1 | 4977,28 | 9614,02 |
| 2,25 | 4977,28 | 10360,61 |
| 2,4 | 5157,12 | 11120,69 |
| 2,55 | 5157,12 | 11894,26 |
| 2,7 | 5157,12 | 12667,82 |
Tabela 1: Parâmetros do reservatório de detenção.
A tabela 2 traz informações dos parâmetros de propagação, o cálculo da vazão está diretamente ligado a diferença de cota, sendo que, até a cota da soleira do vertedouro (1,50m) o orifício atua sozinho, quando a capacidade máxima do reservatório é atingida passa a atuar em conjunto, orifício e vertedouro, extravasando o excesso para garantir a integridade do reservatório e não ocorra transbordamento, sendo importante essa análise ao dimensionar o volume de projeto. Os parâmetros (2S/\(\Delta\)t)+0 e (2S/\(\Delta\)t)-0 ajudam a encontrar a vazão de saída em relação ao tempo (Anexo B).
| O (m³/s) | (2S/Δt)+O (m³/s) | (2S/Δt)-O (m³/s) |
|---|---|---|
| 0 | 0 | 0 |
| 0,212 | 10,921 | 10,496 |
| 0,26 | 14,609 | 14,089 |
| 0,3 | 18,36 | 17,76 |
| 0,336 | 22,107 | 21,435 |
| 0,368 | 25,922 | 25,186 |
| 0,397 | 29,805 | 29,011 |
| 0,425 | 33,687 | 32,838 |
| 0,451 | 37,64 | 36,739 |
| 1,009 | 42,199 | 40,181 |
| 2,008 | 47,198 | 43,181 |
| 3,295 | 52,558 | 45,969 |
| 4,813 | 58,224 | 48,598 |
| 6,531 | 64,09 | 51,028 |
| 8,428 | 70,21 | 53,353 |
| 10,489 | 76,568 | 55,591 |
| 12,7 | 83,077 | 57,677 |
Tabela 2: Parâmetros para o cálculo da propagação.
Com a informação do hidrograma de projeto é possível fazer a tabela 3, para encontrar o valor de (2S/Δt)+O é feito a soma da linha anterior das colunas 4 e 5 (equação \ref{eq:eqcContinuidade3}), já os valores (2S/Δt)-O e O deve ser feito interpolação com o auxílio da tabela 2 e do parametro (2S/Δt)+O, dessa forma achamos a vazão amortecida pelo uso do reservatório.
| índice | tempo (h) | i (m³/s) | \(i_{1}\)+\(i_{2}\) (m³/s) | (2S/Δt)-O (m³/s) | (2S/Δt)+O (m³/s) | O (m³/s) |
|---|---|---|---|---|---|---|
| 1 | 0,1 | 0 | 0 | 0,000 | 0,000 | 0 |
| 2 | 0,2 | 0 | 0,002 | 0,000 | 0,000 | 0 |
| 3 | 0,3 | 0,002 | 0,044 | 0,002 | 0,002 | 0 |
| 4 | 0,4 | 0,042 | 0,31 | 0,043 | 0,046 | 0,001 |
| 5 | 0,5 | 0,268 | 1,106 | 0,333 | 0,353 | 0,007 |
| 6 | 0,6 | 0,838 | 2,66 | 1,356 | 1,439 | 0,028 |
| 7 | 0,7 | 1,822 | 4,812 | 3,783 | 4,016 | 0,079 |
| 8 | 0,8 | 2,99 | 6,966 | 8,098 | 8,595 | 0,169 |
| 9 | 0,9 | 3,976 | 8,549 | 14,273 | 15,064 | 0,268 |
| 10 | 1 | 4,573 | 9,281 | 21,801 | 22,822 | 0,346 |
| 11 | 1,1 | 4,708 | 9,103 | 29,867 | 31,082 | 0,412 |
| 12 | 1,2 | 4,395 | 8,159 | 37,343 | 38,970 | 0,766 |
| 13 | 1,3 | 3,764 | 6,783 | 41,772 | 45,501 | 1,936 |
| 14 | 1,4 | 3,019 | 5,333 | 43,505 | 48,555 | 2,621 |
| 15 | 1,5 | 2,314 | 4,022 | 43,652 | 48,838 | 2,643 |
| 16 | 1,6 | 1,708 | 2,935 | 43,050 | 47,674 | 2,339 |
| 17 | 1,7 | 1,227 | 2,108 | 42,061 | 45,985 | 1,935 |
| 18 | 1,8 | 0,881 | 1,517 | 40,978 | 44,169 | 1,583 |
| 19 | 1,9 | 0,636 | 1,097 | 39,980 | 42,496 | 1,254 |
| 20 | 2 | 0,461 | 0,793 | 38,924 | 41,077 | 0,986 |
| 21 | 2,1 | 0,332 | 0,572 | 37,903 | 39,717 | 0,842 |
| 22 | 2,2 | 0,24 | 0,414 | 36,972 | 38,476 | 0,706 |
| 23 | 2,3 | 0,174 | 0,299 | 36,043 | 37,386 | 0,584 |
| 24 | 2,4 | 0,125 | 0,217 | 35,020 | 36,342 | 0,477 |
| 25 | 2,5 | 0,092 | 0,159 | 33,937 | 35,237 | 0,448 |
| 26 | 2,6 | 0,067 | 0,115 | 32,817 | 34,095 | 0,443 |
| 27 | 2,7 | 0,048 | 0,08 | 31,677 | 32,931 | 0,438 |
| 28 | 2,8 | 0,032 | 0,052 | 30,529 | 31,757 | 0,432 |
| 29 | 2,9 | 0,02 | 0,032 | 29,376 | 30,581 | 0,427 |
| 30 | 3 | 0,012 | 0,018 | 28,230 | 29,408 | 0,421 |
| 31 | 3,1 | 0,006 | 0,009 | 27,096 | 28,248 | 0,415 |
| 32 | 3,2 | 0,003 | 0,004 | 25,979 | 27,106 | 0,409 |
| 33 | 3,3 | 0,001 | 0,001 | 24,883 | 25,984 | 0,404 |
| 34 | 3,4 | 0 | 0 | 23,812 | 24,885 | 0,398 |
| 35 | 3,5 | 0 | 0 | 22,766 | 23,813 | 0,392 |
Tabela 3: Tabela de Propagação.
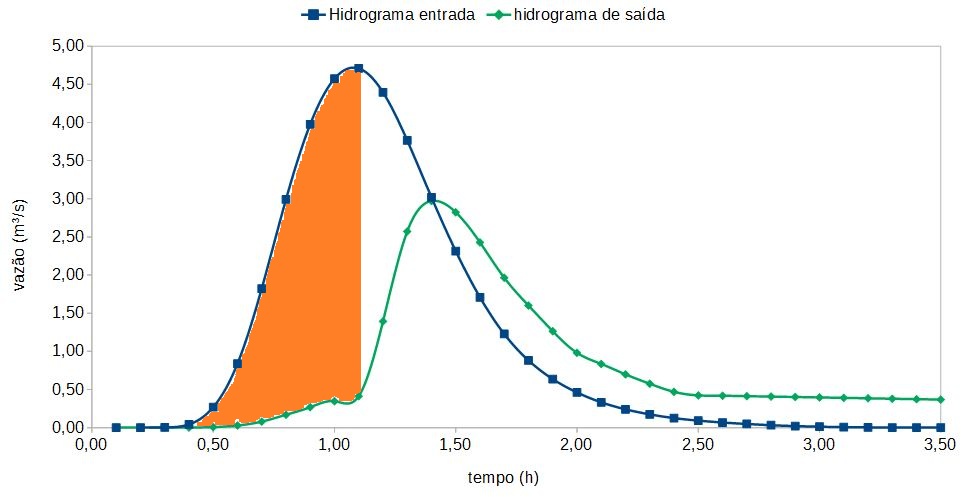
A figura 4 é utilizada pra analisar a diferença do pico da vazão, observe que a vazão efluente máxima ocorre no ponto onde o hidrograma de saída cruza o hidrograma de entrada. Essa é uma característica das propagações de reservatório. No hidrograma de saída o aumento da vazão aconteceu devido a utilização do vertedouro no instante de tempo aproximado de 1,10 horas.
Figura 4: Hidrograma amortecido.
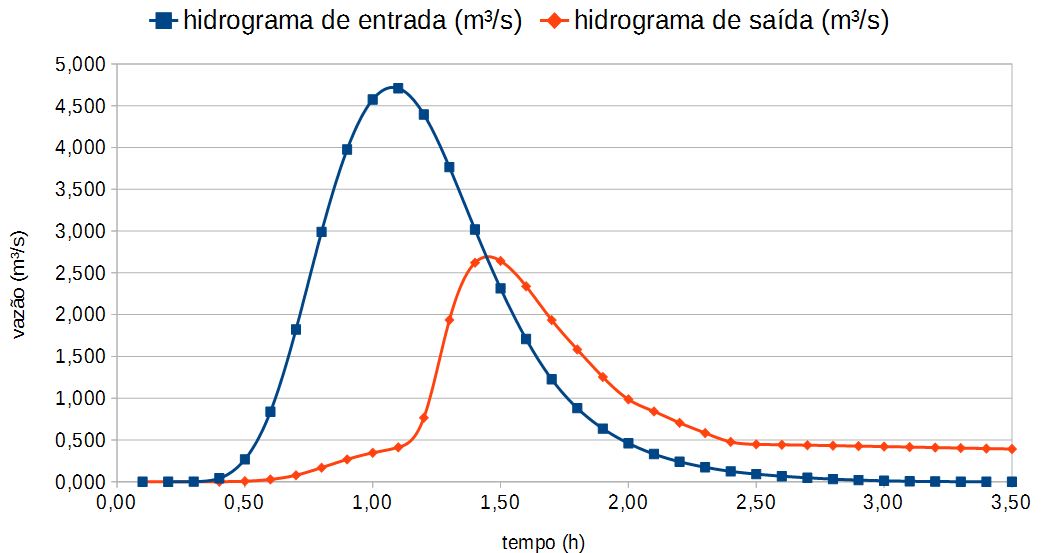
Note também que a vazão efluente máxima de 4,708\(m^3\)/s corresponde a uma elevação máxima de reservatório de aproximadamente 2,1 metros, que pode ser determinado interpolando a taxa de descarga em relação a cota. Essa elevação se tornaria então o nível de água de projeto na bacia de detenção, apesar de passar 60cm cm da cota da soleira, o reservatório está bem dimensionado e não ocorrerá transbordamento.
Finalmente, observe que a propagação resultou em uma redução da vazão efluente máxima de 4,708\(m^3\)/s (entrada) para 2,643\(m^3\)/s (saída). Isso é uma atenuação de 43,86%, obtida pela equação \ref{eq:eqcContinuidade4}. O retardo no tempo é de aproximadamente 24 minutos.
\begin{equation} \label{eq:eqcContinuidade4}\tag{4} \frac{\Delta Q}{Q_{af}} = \left (\frac{Q_{p,af} - Q_{p,ef}}{Q_{p,af}} \right )\times 100 \end{equation}
Onde:
\(\frac{\Delta Q}{Q_{af}}\): diferença de laminação;
\(Q_{p,af}\): Vazão de pico afluente \(m^{3}\)/s;
\(Q_{p,ef}\): Vazão de pico efluente \(m^{3}\)/s.
Planilha
Estou disponibilizando a planilha no Google Sheet e Dropbox para auxiliar no cálculos e gráficos, lembrando que o formato do reservatório é muito importante para o cálculo.
Código
Feito a planilha, então vá ao meu respositório do Github e siga as instruções do arquivo Readme.md, o código retorna os valores da interpolação da vazão amortecida.
Fontes
BUTLER, S. Engineering Hydrology. [S.l.]: Prentice-Hall, 1957.
GRIBBIN, J. Introdução à hidráulica, hidrologia e gestão de águas pluviais. [S.l.]: CengageLearning, 2009. ISBN 9788522106356.
PULS, L. Flood Regulation of the Tennessee River. [S.l.]: 70th Congress, !st Session, U.S.Government Printing Office, 1928.
PULS, L. Bureau of Reclamation Manual. [S.l.]: U.S. Department of the Interior, Denver,1947.
TUCCI, C. Hidrologia: Ciência e Aplicação. [S.l.]: Editora da Universidade, UFRGS, 2007.(Coleção ABRH de Recursos Hídricos). ISBN 9788570259240.
Anexo A
Figura 5: cota x volume.
Figura 6: cota x vazão.
Figura 7: volume x vazão.
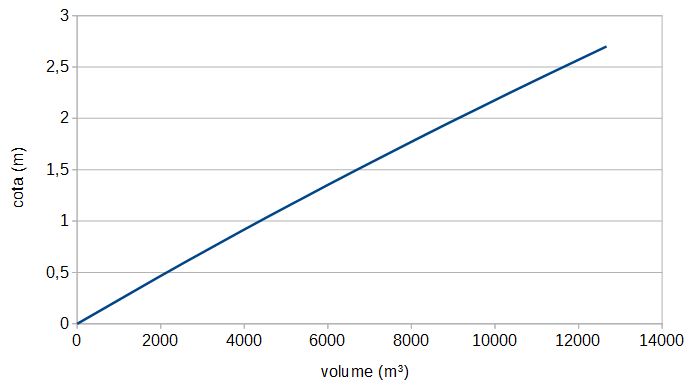
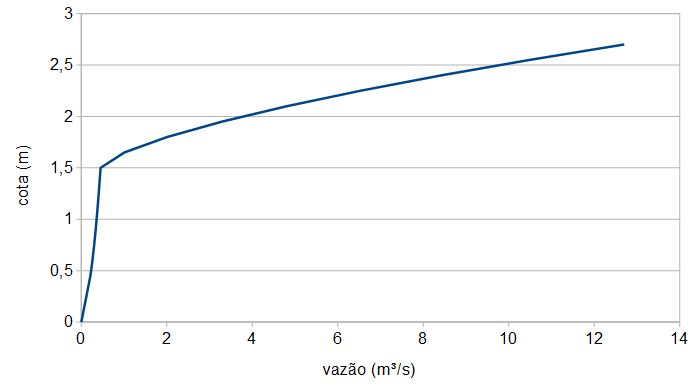
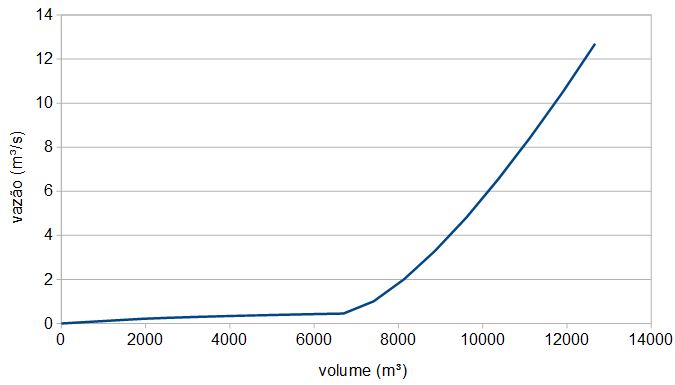
Anexo B
Figura 8: Parâmetros da reservatório de detenção.