Método Soil Conservation Service - SCS
1. Separação do escoamento
A separação do escoamento é a etapa do método SCS que consiste na determinação volume de água que entra na bacia através da precipitação que será escoado superficialmente, através de um balanço hídrico. A precipitação que cai sobre uma bacia hidrográfica pode seguir quatro caminhos potenciais: parte da precipitação é interceptada pela vegetação e evaporada para a atmosfera; parte cairá sobre o solo e irá evaporar; parte irá infiltrar no solo; e o restante irá escoar superficialmente na bacia. A quantidade de precipitação e o parâmetro Curve Number (CN), irão determinar a quantidade de água que irá escoar na bacia e encontrar os cursos d’água superficiais.
O parâmetro CN ou número de escoamento da bacia hidrográfica retrata as condições da camada superficial do solo, que pode variar desde uma cobertura muito permeável até uma cobertura completamente impermeável, e da camada superior de solo, que pode ter capacidade de infiltração alta ou baixa.
O CN é um parâmetro adimensional e seu valor varia entre 0 e 100, sendo que 0 corresponde a um solo com capacidade de infiltração infinita e 100 corresponde a um solo totalmente impermeável (COLLISCHONN; DORNELLES, 2013).
Esta separação do escoamento no Método SCS é realizada através da a Equação:
\begin{equation} \label{eq:VolumeSuperficial}\tag{1} V = \frac{(P - I_{a})^{2}}{P+S-I_{a}} \end{equation}
Onde:
V: volume superficial acumulado (mm);
P: precipitação total acumulada (mm);
\(I_{a}\): perdas iniciais (mm);
S: capacidade máxima de armazenamento da camada superior do solo (mm). \
O parâmetro \(I_{a}\) representa as “perdas” de água que ocorrem antes do escoamento começar, ou seja, é a porção do volume de água precipitado que não é escoado superficialmente, seja por interceptação na vegetação, evaporação, infiltração ou outras causas. Esse é um parâmetro bastante variável, mas geralmente se relaciona com parâmetros do solo e da cobertura da bacia. As perdas iniciais pode ser estimado para as condições médias como sendo 20% da capacidade de armazenamento do solo (equação \ref{eq:PerdasIniciais}).
\begin{equation} \label{eq:PerdasIniciais}\tag{2} I_{a} = 0,2.S \end{equation}
A determinação do parâmetro foi estabelecida através de uma escala onde a variável é o parâmetro CN. A Equação \ref{eq:CapacidadeMaximaArmazenamentoSolo} representa relação entre o parâmetro e a variável e está convertida para unidades métricas.
\begin{equation} \label{eq:CapacidadeMaximaArmazenamentoSolo}\tag{3} S = \frac{25400}{CN} - 254 \end{equation}
2. Propagação superficial
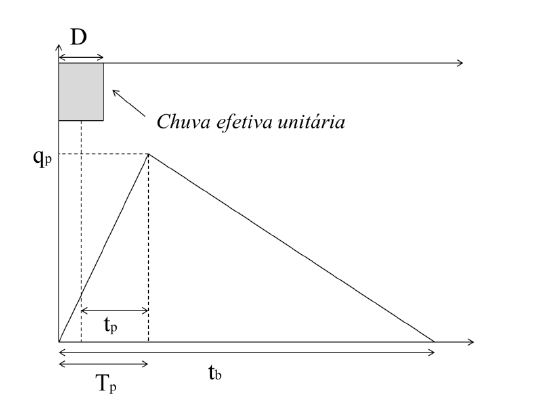
O modelo SCS utiliza o hidrograma unitário sintético triangular, figura 1. A forma do hidrograma unitário depende da área da bacia hidrográfica, da duração da chuva efetiva unitária e do tempo de concentração da bacia.
Tempo de concentração é o tempo que leva para que o escoamento chegue até um ponto de interesse, a partir do ponto hidraulicamente mais distante. No caso desse modelo, o ponto de interesse é o local onde será posicionado o reservatório.
Segundo USDA (1986, o tempo de concentração da bacia (\(T_c\)) é um parâmetro crítico do modelo SCS. Esse parâmetro influencia na forma e no pico do hidrograma de escoamento.
Segundo Silveira (2005), o tempo de concentração é um parâmetro hidrológico difícil de ser estabelecido com critério pelos projetistas, pois há pouca informação sobre a aplicabilidade das diversas fórmulas empíricas disponíveis. Este exemplo usa a fórmula do tempo de concentração de Schaake, sendo utilizada para bacias urbanas menores que 0,7\(km^2\).
\begin{equation} \label{eq:tempo-de-concentracao}\tag{4} T_{c} = 0.0828.(L^{0.24}).(S^{-0.16}).(A_{imp}^{-0.26}) \end{equation}
Onde:
L: comprimento do coletor pluvial ou canal principal (km);
S: declividade média do coletor pluvial ou canal principal (m/m);
\(A_{imp}\): fração de área impermeável, variando entre 0 e 1 (adimensional).
O hidrograma unitário é definido por cinco parâmetros: a duração da chuva efetiva unitária (D); o tempo de pico \((t_{p})\), que é o tempo desde a metade da duração da chuva efetiva unitária até o pico de vazão do hidrograma unitário, calculado pela Equação:
\begin{equation} \tag{5} t_{p} = 0,6 . T_{c} \end{equation}
Onde:
\(T_{c}\): tempo de concentração da bacia (horas).
O tempo de subida do hidrograma (\(T_{p}\)), é o tempo desde o início do evento chuvoso até o pico do hidrograma unitário, calculado pela Equação:
\begin{equation} \tag{6} T_{p} = t_{p} + \frac{D}{2} \end{equation}
Onde:
\(T_{p}\) : Tempo de subida do hidrograma (horas);
D: Duração da chuva efetiva unitária (horas).
O tempo de base (\(t_{b}\)), é o tempo desde o início do evento chuvoso até o final do escoamento superficial no exutório da bacia, calculado pela Equação:
\begin{equation} \tag{7} t_{b} = T_{p} + 1,67.T_{p} \end{equation}
A vazão de pico do hidrograma unitário (\(q_{p}\)), calculada pela Equação:
\begin{equation} \tag{8} q_{p} = \frac{0,208.A.P}{T_{p}} \end{equation}
Onde:
A: Área da bacia hidrográfica (\(km^{2}\));
P: Precipitação (mm).
A chuva efetiva unitária deve ter uma duração 5 a 10 vezes menor que o tempo de concentração da bacia.
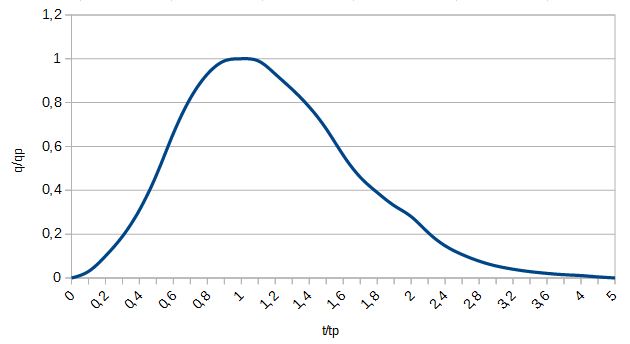
3. Hidrograma unitário adimensional
Usando o hidrograma unitário adimensional (figura 2) pode construir qualquer distribuição de chuva, dividindo em número de elementos da precipitação efetiva unitária e desenhando o hidrograma unitário para cada um. O hidrograma resultante seria então a soma de todos os hidrogramas unitários. O SCS desenvolveu uma base de dados de hidrogramas unitários a partir de parâmetros que descrevem as características das bacias hidrográficas, bem como os padrões de precipitação para locais geográficos específicos.
4. Exemplo prático
Na tabela 1 foi utilizado o tempo de duração de 60 minutos, tempo de retorno de 50 anos e CN da bacia contribuinte de 80, correspondente a uma chuva intensa em Fortaleza.
| índice | td(min) | i(mm/h) | td(h) | precipitação(mm) | precipitação acum.(mm) | precipitação excedente – acum(mm) | precipitação excedente em cada tempo(mm) |
|---|---|---|---|---|---|---|---|
| 1 | 6 | 37,1 | 0,1 | 3,71 | 3,71 | 0 | 0 |
| 2 | 12 | 49 | 0,2 | 4,9 | 8,61 | 0 | 0 |
| 3 | 18 | 68,7 | 0,3 | 6,87 | 15,48 | 0,117 | 0,12 |
| 4 | 24 | 105,5 | 0,4 | 10,55 | 26,03 | 2,313 | 2,2 |
| 5 | 30 | 188,8 | 0,5 | 18,88 | 44,91 | 10,84 | 8,53 |
| 6 | 36 | 137,6 | 0,6 | 13,76 | 58,67 | 19,304 | 8,46 |
| 7 | 42 | 83,9 | 0,7 | 8,39 | 67,06 | 25,072 | 5,77 |
| 8 | 48 | 57,5 | 0,8 | 5,75 | 72,81 | 29,231 | 4,16 |
| 9 | 54 | 42,4 | 0,9 | 4,24 | 77,05 | 32,389 | 3,16 |
| 10 | 60 | 32,9 | 1 | 3,29 | 80,34 | 34,888 | 2,5 |
Tabela 1: Precipitação de projeto
A Figura 3 mostra a relação da precipitação total e a parcela de precipitação efetiva (que se transforma em escoamento superficial direto).
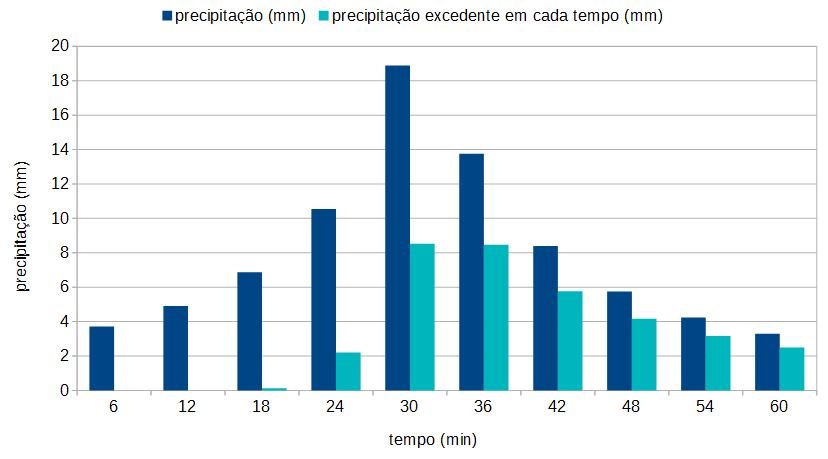
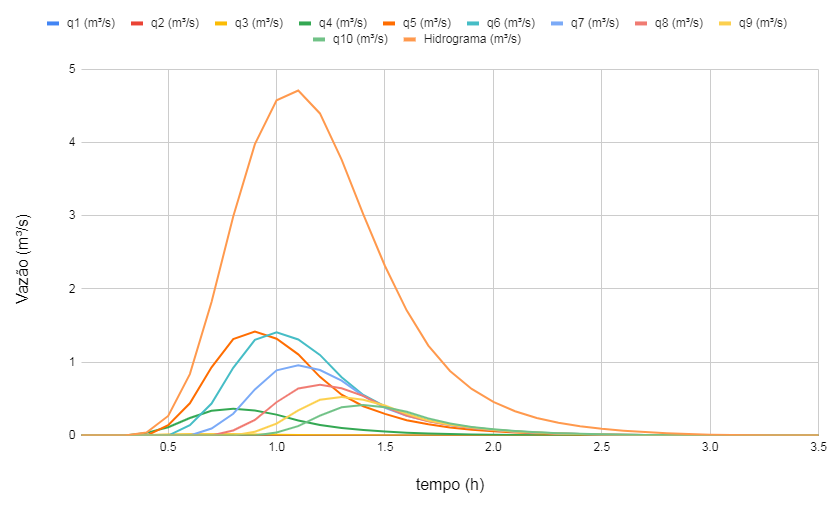
Para obter o hidrograma de projeto deve-se associar a parcela de cada bloco que escoa a uma determinada precipitação efetiva unitária, fixando o tempo de duração, acha-se o hidrograma unitário dimensional, para então descobrir a vazão e o hidrograma do bloco. Aplicando os princípios da proporcionalidade e da superposição é possível calcular os hidrogramas resultantes de eventos complexos, a partir do hidrograma. Este cálculo é feito através da convolução das ordenadas de cada bloco. O hidrograma é, normalmente, definido como uma função em intervalos de tempo discretos. Na figura 4, o tempo de concentração foi determinado pela fórmula de Schaake, aplicável para bacias urbanas menores que 0,7km², adotando a área da bacia 40ha, área impermeável de 0,5 e declividade de 1% para uma chuva com tempo de duração de 60 minutos. Os valores q1, q2,…,\(q_{n}\) se referem à aplicação de cada bloco da precipitação excedente em cada tempo, que será dividido pela precipitação e então multiplicado pela vazão do hidrograma unitário.
 Figura 4: Hidrograma de projeto
Figura 4: Hidrograma de projeto
Está disponível no Google Sheet e no Dropbox a planilha e o vídeo (figura abaixo) que explica o passo a passo do método.
Fonte
COLLISCHONN, W.; DORNELLES, F. Hidrologia para engenharia e ciências ambientais.2013.
USDA, S. Urban hydrology for small watersheds. 1986. 2–6 p.
SILVEIRA, A. L. L. da. Desempenho de formulas de tempo de concentração em baciasurbanas e rurais. 2005. 5–23 p.